Summary

搜索

对于数组范围类：应该考虑为数字个数而不是范围，否则边界条件容易混淆

将遍历搜索改成搜索的时候直接找到一条路径

11 container with most water: N^2 -> N

15 3sum: N^3 -> N^2

3sum：不要设计得很复杂（分为很多步骤，并没有实际优化复杂度），要看本质

注意：while()循环跳过的时候，第一个条件应该是界限

While(r < size && n[r] == ...) 而不是反过来

注意best的初值，要么是最值的反面，要么随机设置成一个初值

注意：不要写错变量名

注意：边界条件，如top之前检查stack大小

DP

推导公式的时候可以用分类，保证不重不漏 （22 Generate Parentheses）
32 Longest Valid Parentheses

priority_queue

23 merge k sorted lists

考虑清楚递归/循环每一次的情况

24 swap nodes in pairs

链表的处理：比如swap两个，反转，确定循环节，prev, curr

注意：思维严密，如28 strstr
开始思路是顺着找，m++，但是应该O^2，没有考虑到
"mississippi"
"issip"
的情况

bianry search

34 Find First and Last Position of Element in Sorted Array

在DFS记录路径/输出排列的时候，用push_back和pop_back来避免copy

双指针夹

1/container with most water/Trapping Rain Water

思路：对于overlap问题，按照起始点排序

391/room
763/ Partition Labels

对于二维问题，投影到两个一维

391

391: 用pair作为map的key
如果是unordered 需要一个hash
std::hash()(1)

struct pair_hash
{
template<class T1, class T2>
std::size_t operator() (const std::pair<T1, T2>& p) const
{
auto h1 = std::hash<T1>()(p.first);
auto h2 = std::hash<T2>()(p.second);
return h1 ^ h2;
}
};
struct pair_cmp
{
template<class T1, class T2>
std::size_t operator() (const std::pair<T1, T2>& p1,const std::pair<T1, T2>& p2) const
{
return (p1.first == p2.first)?(p1.second < p2.second):(p1.first<p2.first);
}
};

一般需要O(N)的算法，考虑两个指针夹，或者前后扫两遍

238

对于子序列和的问题，还可以求prefix

974
Subarray Sums Divisible by K
子序列和可以表示为两个prefix相减

quick select/sort复习

215

遇到限定为A-Z a-z的，可以考虑对每个字母bitmap

76

搜索+存储 从上到下的DP

139
搜索的时候考虑剪枝，尽量减少重复计算，word break的时候，如果已经尝试了某个点无法继续，就记录下来

对于搜索，如果确定插入是按照顺序的，不需要树，直接二分搜索就行

981

DP

322
DP的两种方法：
从上到下：DFS+table存储
从下到上，先算小的再算大的

同样的两种DP：

第三道是⽐比较少⻅见的背包问题，⼤大意是有n套丛书，每套书包含X本书，按套卖，每套价值Y元。所以有两个 等⻓长input array分别代表每套书包含⼏几本书和每套书卖多少钱。另⼀一个input是int，代表你的预算。求最多 能买多少本书。

注意好的DP函数
换硬币：坏的DP函数，F(x) = min(F(i),F(x-i))
好的DP函数，F(x) = min(F(coins[i]), F(x-coins[i]))

*两维DP
climb the hill
https://blog.csdn.net/v5zsq/article/details/79605704
Split Array Largest Sum
L410
Campus Bikes
L1130

二叉树的序列化

297
注意只有数字不同才可以用pre+in order恢复
不然需要层次遍历来序列化

正确的序列化方法应该是DFS，记录null child

善用hash table

a: a,b,c,d,e,f
b: e,a,b,c,h,t
没有重复，找最长匹配
LC939 Minimum Area Rectangle

LC953 Verifying an Alien Dictionary

Input: words = ["hello","leetcode"], order = "hlabcdefgijkmnopqrstuvwxyz"
Output: true
Explanation: As 'h' comes before 'l' in this language, then the sequence is sorted.

LC1055 Shortest Way to Form String

Input: source = "abc", target = "abcbc"
Output: 2
Explanation: The target "abcbc" can be formed by "abc" and "bc", which are subsequences of source "abc".

注意merge two sorted array时的back tracing

如果要用两个sorted array做join，需要back tracing
比如 1,1,3,4 1,1,2,3，对于1，需要有4个结果

对于O(1)优化，考虑用stack

比如candy crash
比如对数组中元素，找到右边第一个小于等于它的元素 (L503)

tree的LCA

思想：Binary search + greedy验证

将数组分成n份，每个子数组的和的最大的最小是多少
LC410

1048，可以用DP解，就不要用图+DFS

Summary of search

  1. BFS

如果要记录深度，可以用两个queue，同时存深度
或者用两个queue轮换，但是每次循环把queue弹空

queue<Node> q;
unordered_set<Node> visited;
q.push();
while(!q.empty()) {
Node curr = q.front();
q.pop();
visited.insert(q);
if(q == target) {
return;
}
// visit it
for(all children c) {
if(s.find(c) == s.end()) {
q.push(c);
}
}
}
  1. DFS
    用迭代DFS
    剪枝（DP记录最优）
    记录路径的时候用同一块空间，return 之前恢复原状
    排列

LC39 Combination Sum

Input: candidates = [2,3,6,7], target = 7,
A solution set is:
[
[7],
[2,2,3]
]
Input: candidates = [2,3,5], target = 8,
A solution set is:
[
[2,2,2,2],
[2,3,3],
[3,5]
]

写法1：每次DFS的时候遍历每个candidate
写法2：对于每个candidate，在DFS中选择要或者不要

LC46 Permutations

Input: [1,2,3]
Output:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]

每次DFS的时候确定一位

void rec_search(Node) {
if(visited(Node)) {
return;
}
//剪枝返回
// visit
for(all children c) {
if(!visited(c)) {
rec_search(c);
}
}
}
  1. A* search / dijkstra
    是BFS的扩展，不是用队列，而是有选择地找出最好的
    A* value of f(v) [f(v) = h(v) + g(v)] - where h is the heuristic [hjuˈrɪstɪk] and g is the cost so far
    dijkstra是A的特殊形式，当heuristic = 0的时候
    如果h是admissible的，即永远小于最优解的从当前点到终点的cost，那么A    可以返回最优且一定能找到

http://theory.stanford.edu/~amitp/GameProgramming/AStarComparison.html
https://blog.csdn.net/geyes/article/details/82891433

Trick

找到下一个排列

4 2 5 3 1 -> 4 3 1 2 5
从右到左，找到第一个下降的位置，然后找右边最小的比它大的位置替换，然后reverse右边

std::next_permutation
std::prev_permutation

有parent指针的树遍历

一道题 给left right parent 指针，不用栈 中序遍历

存一个flag，表示上次是从左子树上去的，还是从右子树上去的，还是才父节点下来的

删除一个array不一定需要O(N)

如果没有sorted要求，可以直接O(1)交换最后一个，然后decrease size

Graph

directed graph: strong connected / weak connected
undirected graph: connected

acyclic/cyclic graph
[ˌeɪˈsaɪklɪk]
[saiklik]

represent

  1. adjacency matrix O(V^2)
  2. adjacency list O(V+E)

topological sorting

[,tɑpə'lɑdʒɪkl]
O(E+V)

queue<Node> q;
vector<int> indegree;
initialize indegree list
push all zero indegree to q
while(!q.empty()) {
dequeue a node
// visit
for each adjacent n:
--indegree[n]
if(indegree[n] == 0) {
enqueue n
}
}
if(visited count != total count) {
has a cycle
}

shortest path

if negative-cost cycle exists, result is undefined
if unweighted, then BFS O(V+E)

queue<Node> q;
unordered_set<Node> visited;
q.push();
while(!q.empty()) {
Node curr = q.front();
q.pop();
visited.insert(q);
// visit it
for(all children c) {
if(s.find(c) == s.end()) {
q.push(c);
}
}
}

if weighted but no negative cost edge
dijkstra [ˈdɑɪkstɹə/]
如果扫描所有节点得到最小值，时间复杂度 O(E+V^2)，适合dense
如果sparse，用priority queue 可以每次都push一个新的，然后pop都时候找到一个unknown的， 复杂度O(ElogV+VlogE)
用fibonacci heap，O(E+VlogV)

c++实现的时候，用一个N+1大小的min_dis数组和一个priority queue，和一个N+1大小的adjacency list
queue里面存（点，距离）对
min_dis为 INT_MAX就是不确定
初始化push进开始点和0
然后pop直到一个不确定的点
然后确定这个点
更新所有不确定的邻居

while(true) {
v = smallest unknown distance
set v as known
for each adjacent n:
if(n is unknown) {
update distance of n
}
}

if negative cost edge exists
Bellman-Ford
O(EV)

enqueue start point
while(queue is not empty) {
n = dequeue
for each adjacent v:
update v
if v is not in queue
enqueue v
}
for(int k = 1 ; k <= n - 1 ; k ++)
{
for(int i = 1 ; i < m ; i ++)
{
if(dis[v[i]] > dis[u[i]] + w[i])
dis[v[i]] = dis[u[i]] + w[i] ;
}
}

if no cycle
拓扑排序后找max
从前到后找最早完成时间
从后到前找最晚完成时间
DP?

Kosaraju algorithm

find strongly connected components
Kosaraju
原图G:
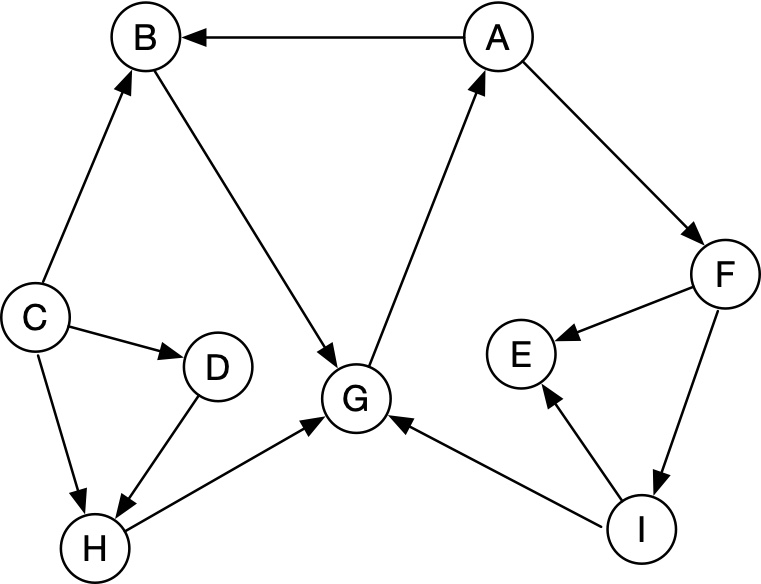
IMAGE
对取反之后对图G'的DFS顺序为A G B C H D I F E
DFS结束的顺序为 C B D H F I G A E
对原图访问的顺序为 E A G I F H D B C

访问 E：{E}
访问 A：{A B G F I}
访问 H：{H}
访问 D：{D}
访问 C：{C}

所以得到五个连通图：{E}, {A B G F I}, {H}, {D}, {C}

/* Find Strongly Connected Components - Tarjan*/
对原图G取反得到G'
对G'进行DFS，获得DFS访问结束之后的出栈顺序
按照出栈顺序的逆序对原图G进行DFS，每次DFS结束都是一个SCC

Tarjan algorithm

对于tarjan，num(v)代表被DFS到的顺序，low(v)代表

  1. num(v)
  2. 所有子节点的low
  3. 所有back edge的num
    中的最小

back edge不包括从儿子指向父亲

所以low代表通过任意搜索树上的边和至多一条back edge可以到达的最小

find strongly connected components
find circle

find articulation point
对于点v和儿子c，low(c)>=num(v)，则v是articluation point
find critical path
对于点v和儿子c，low(c)>num(v)，则v->c是critical path

Euler path

[ˈɔɪlər]
O(E+V)
联通且所有节点度数为偶数，一定有

Hamiltonian cycle problem/travel salesman problem

['hæmiltən]
https://www.cnblogs.com/zquzjx/p/9148135.html
NP-hard, Brute-force，next_permutation

用两个heap实现维护中间值

一个max一个min

slow and fast pointer

LC109 可以用来找linked list里面的中间值

Dijkstra

LC743

There are N network nodes, labelled 1 to N.
Given times, a list of travel times as directed edges times[i] = (u, v, w), where u is the source node, v is the target node, and w is the time it takes for a signal to travel from source to target.
Now, we send a signal from a certain node K. How long will it take for all nodes to receive the signal? If it is impossible, return -1.

Input: times = [[2,1,1],[2,3,1],[3,4,1]], N = 4, K = 2
Output: 2

class Solution {
public:
int networkDelayTime(vector<vector<int>>& times, int N, int K) {
unordered_map<int, vector<pair<int,int>>> adj(N+1);
for(const auto & v : times) {
adj[v[0]].push_back(make_pair(v[1],v[2]));
}
vector<int> min_dis(N+1, INT_MAX);
auto cmp = [](const pair<int,int> &p1, const pair<int,int> &p2) {return p1.second>p2.second;};
priority_queue<pair<int,int>, vector<pair<int,int>>, decltype(cmp)> q(cmp);
q.push(make_pair(K, 0));
while(!q.empty()) {
pair<int,int> p = q.top();
q.pop();
if(min_dis[p.first] != INT_MAX) {
continue;
}
min_dis[p.first] = p.second;
for(const auto & v : adj[p.first]) {
if(min_dis[v.first] == INT_MAX) {
q.push(make_pair(v.first, v.second + p.second));
}
}
}
int res = -1;
for(int i=1;i<=N;++i) {
if(min_dis[i] > res) {
res = min_dis[i];
}
if(min_dis[i] == INT_MAX) {
return -1;
}
}
return res;
}
};

TODO

743/126

O(N) solutions: Two pointer / Stack / Two pass

LC42 Trapping rain water
IMAGE
对于每个点，找左边的最大和右边的最大中较小的一个
用two pointer的话，每次移动更低的指针，

11 container with most water
two pointer

15 3sum
two pointer

VMwareOA
IMAGE
对于每个点，找到左边所有同样点的距离和右边所有同样点的距离的和
扫两遍，存一个map，key是点的数值，value是（点出现的次数，点的index和）

Stack

Candy crash

TwitterOA
找每一个数右边第一个小于等于它的数字
对于每一个树，和栈顶比较
如果栈顶小于等于它，那么直接入栈

两点之间的距离等于他们到root的距离和减去两倍的LCA到root的距离

带weight的树，O(N)求一组query的结果（每一个query是一个点对，求距离）

又例：
VMwareOA
两点之间的距离等于他们到0的距离的差

Divide and conquer

给定一个binary tree, inplace转换成double linked list
举例： 
            1
          /   \
        2       3  
        \      / \
         4    5   6
        /
       7

转换成
2<->7<->4<->1<->5<->3<->6

'''
class Node:        
    value, left, right = None, None, None

    def __init__(self, value, left = None, right = None):
        self.value, self.left, self.right = value, left, right
'''

然后 return head
void build_list(Node *root, Node **left, Node **right) {
Node *left_left, left_right, right_left, right_right;
if(root->left != NULL) {
build_list(root->left, &left_left, &left_right);
root->left = left_right;
}
else {
left_left = root;
}
if(root->right == NULL) {
build_list(root->right, &right_left, &right_right);
root->right = right_left;
}
else {
right_right = root;
}
*left = left_left;
*right = right_right;
}

随机采样

对于一个数列，可以依次确定每一个点
对于一个stream，可以存一个10的buffer，对于前10个都保存
对于第i个，有10/i可能保存（随机替换），否则直接丢弃

Bracktracing / DFS

https://leetcode.com/explore/learn/card/recursion-ii/472/backtracking/2793/
Robot cleaner

不要把题想复杂

LC1055 Shortest Way to Form String

Input: source = "abc", target = "abcbc"
Output: 2
Explanation: The target "abcbc" can be formed by "abc" and "bc", which are subsequences of source "abc".

直接O(N)搜索就行

思想：什么东西已经是不必要的，什么时候需要及时删除？

Sliding Window Maximum的deque解

思想：lazy deletion

比如dijkstra的heap，比如Sliding Window Maximum的heap解

思想：分析复杂度的时候，可以按照每个元素的角度分析

比如对于sliding window，或者lazy deletion，每个元素最多添加一次删除一次，所以是O(N*p)，p是每个元素最多的时间复杂度

思想：如何分类

LC828. Unique Letter String
可以按照subarray的起始点分类，也可以按照每一个元素分类

LC939. Minimum Area Rectangle
可以用对角线两个点来确定一个矩形

LC552. Student Attendance Record II
注意分类，先按照有没有A分类，然后按照长度分类，地推

思想：理清思路，想好证明为什么是对的

LC41. First Missing Positive

Input: [3,4,-1,1]
Output: 2

最小的消失的数肯定在1~n范围内，如果一个数i存在，那么一定会在对应的i-1位置上，那么结果一定是对的

反转链表

思想：先考虑brute force，第一是为了确定上界，第二是为了考虑哪里有重复计算（能不能用空间换重复计算？）

比如 LC828. Unique Letter String
找到所有的subarray有O(N^2)，验证每一个subarray有O(N)，所以最坏O(N^3)
想到验证长subarray的时候，也可以顺便验证短的，就可以验证以i点开头的所有subarray的结果，就是O(N^2)
进一步优化，对于每一个i点开头的所有subarray，如果可以比O(N)更快，就可以更好

Array

Fixed Sized Sliding Window

Sliding Window Median 60%

Sliding Window Median
可以用two heap，也可以用multiset

Sliding Window Maximum
可以用deque
次优解是用heap + lazy deletion

Dynamic Sliding Window / Continuous Subarray

LC713 Subarray Product Less Than K

Input: nums = [10, 5, 2, 6], k = 100
Output: 8
Explanation: The 8 subarrays that have product less than 100 are: [10], [5], [2], [6], [10, 5], [5, 2], [2, 6], [5, 2, 6].
Note that [10, 5, 2] is not included as the product of 100 is not strictly less than k.

LC992 Subarrays with K Different Integers

Input: A = [1,2,1,2,3], K = 2
Output: 7
Explanation: Subarrays formed with exactly 2 different integers: [1,2], [2,1], [1,2], [2,3], [1,2,1], [2,1,2], [1,2,1,2].

LC340 Longest Substring with At Most K Distinct Characters

Input: s = "eceba", k = 2
Output: 3
Explanation: T is "ece" which its length is 3.

LC992和LC159思路类似，都是维护一个sliding window，然后用一个map保存table里面的内容（key -> element, value -> count）
992稍微复杂一些，需要维护两个sliding window，这两个window右边是对齐的，分别表示从左边到右边有K个数字的最大窗口和最小窗口

LC325 Maximum Size Subarray Sum Equals k

LC76 Minimum Window Substring

LC152. Maximum Product Subarray
是DP

LC828. Unique Letter String

Input: "ABC"
Output: 10
Explanation: All possible substrings are: "A","B","C","AB","BC" and "ABC".
Evey substring is composed with only unique letters.
Sum of lengths of all substring is 1 + 1 + 1 + 2 + 2 + 3 = 10

Input: "ABA"
Output: 8
Explanation: The same as example 1, except uni("ABA") = 1.

考虑按照subarray的起点分类

考虑按照每一个元素被几个subarray包含分类（左边界几种可能，右边界几种）
对于每一个字母，边界最远到达字符串结束或者下一个同类字符位置
比如 bdabbabbb，中间的a的左边界最多到第一个a，有3种，右边界到底，最多4种，一共有12个subarray包括了第二个a

Incontinuous Subarray

Find Next or Previous element in Array

Rain Water
Next equal or greater than
LC315 Count of Smaller Numbers After Self(??)

Split Array

Range / Overlap

google下雨
安排会议

Palindromic

LC5 Longest Palindromic Substring

Input: "babad"
Output: "bab"
Note: "aba" is also a valid answer.

回文有两种方法
DP P(i,j) = true 如果substring [i,j]是回文的
然后P(i,j) = (P(i+1,j-1) && Si == Sj)
base case: P(i, i) = true P(i, i+1) = Si == Si+1

还有从中间扩展
都是O(N^2)

Parenthesis

Permutation / Combination

LC552. Student Attendance Record II
DP即可

2-D Coordinate

可以按照对角线分，也可以投影到两个维度

LC939. Minimum Area Rectangle
直接遍历每一种对角点就行了

Matrix

Tree

Binary Tree Inorder Traversal

在完全二叉树的最后一层做binary search：把传统的binary search的寻址方式改一下
数完全二叉树一共有几个节点：先确定深度，然后DFS确定最后一个元素的位置
给一个只有结构的二叉树和inorder array，重新填入值

序列化和反序列化

Segment Tree

Sliding Window Median 60%

Iterative Traversal

LC145 Binary Tree Postorder Traversal

summary
对于iterative traversal，一般方法是用一个stack，和一个指针
一个node有两次被访问的时候，第一次是指针指向它，然后压栈的时候，此时子树都没有访问，压栈之后指针指向左子树或者右子树
第二次是弹出的时候（当第一个访问的子树已经到底，开始弹出），此时压栈时候选择的子树已经访问完，指针应该指向另一个子树

对于preorder，在压栈的时候visit，然后指针指向左子树
弹出的时候指针指向右子树

对于inorder，压的时候不访问，然后指针指向左子树
弹出的时候visit，然后指针指向右子树

对于树的访问，不要像递归一样考虑单个子树（先左边完成，然后中间，然后右边）
而是考虑成单个点，这个点一定会被访问，而且是在左右子树都没有访问的时候（preorder）
在左子树访问完的时候（inorder）

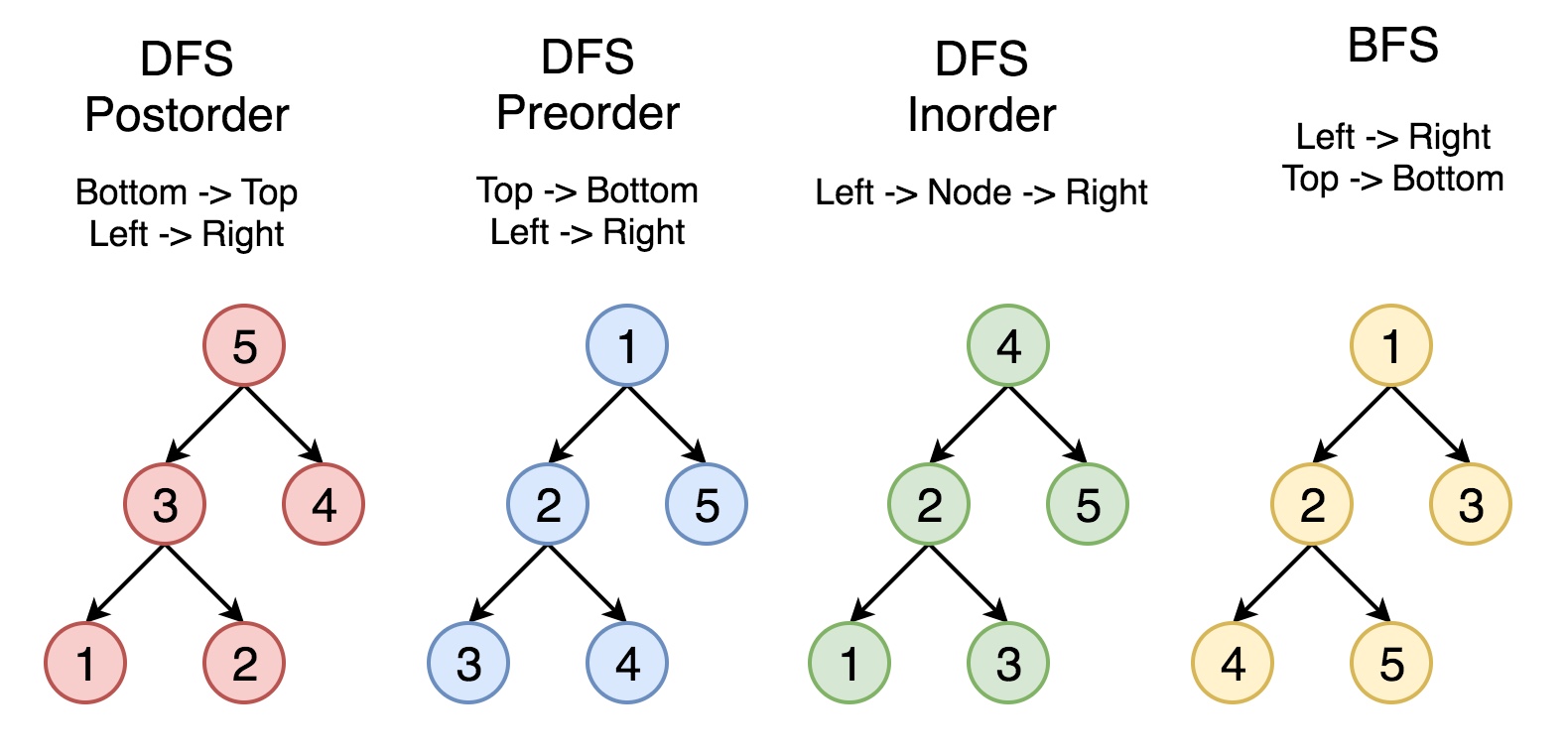
IMAGE

/* preorder/inorder traversal */
stack<int> s;
TreeNode *p = root;
while(!s.empty() || p!=nullptr) {
if(p!=nullptr) {
stack.push(p);
visit(p); // preorder的访问时间
p=p.left;
}
else {
p = stack.top();
stack.pop();
// inorder的访问时间
p = p.right;
}
}
/* preorder */
stack<int> s;
s.push(root);
while(!s.empty()) {
TreeNode *p = s.top();
s.pop();
visit(s);
if(p.left!=nullptr) {
s.push(p.left);
}
if(p.right!=nullptr) {
s.push(p.right);
}
}
/* inorder */
stack<int> s;
TreeNode *p = root;
while(!s.empty()||p!=nullptr) {
while(p!=nullptr) {
s.push(p);
p=p.left;
}
p=s.top();
s.pop();
visit(p);
p=p.right;
}

对于postorder，访问顺序等于preoder一个左右子树调换的树的反向
所以可以

/* postorder traversal */
stack<int> s;
TreeNode *p = root;
while(!s.empty() || p!=nullptr) {
if(p!=nullptr) {
stack.push(p);
visit_last(p); // preorder的访问时间
p=p.right;
}
else {
p = stack.top();
stack.pop();
p = p.left;
}
}

如果不用这个trick

/* postorder traversal*/
stack<pair<TreeNode*,bool>> s;
TreeNode *p = root;
vector<int> ans;
while(!s.empty() || p!=nullptr) {
if(p!=nullptr) {
s.push(make_pair(p,false));
p=p->left;
}
else {
p = s.top().first;
bool right_visited = s.top().second;
s.pop();
if(right_visited) {
ans.push_back(p->val);
p=nullptr;
}
else {
s.push(make_pair(p, true));
p = p->right;
}
}
}

Graph

Search (BFS/DFS)

LC1036 Escape a Large Maze

Normal BFS

LC490. The Maze

Input 1: a maze represented by a 2D array

0 0 1 0 0
0 0 0 0 0
0 0 0 1 0
1 1 0 1 1
0 0 0 0 0

Input 2: start coordinate (rowStart, colStart) = (0, 4)
Input 3: destination coordinate (rowDest, colDest) = (4, 4)

Output: true

Explanation: One possible way is : left -> down -> left -> down -> right -> down -> right.

BFS可以，但是DFS不行，因为在此题中，位置是唯一状态，与如何到达该位置无关
DFS+pruning（存position+direction）应该也可以

由此题开始，BFS和DFS的本质区别？
此题就是在一个有向图中搜索某一个点，由于和路径无关，只是找一个点，所以BFS比较合适
在图中DFS，任何一个时刻的状态是一条路径，而BFS，状态是一个波面和一个访问的点

DFS+pruning

LC490. The Maze
这题DFS+pruning可能也可以，但是normal BFS最方便

Dijkstra

LC505. The Maze II

Bidirectional BFS

Knight's Shortest Path on an Infinite Chessboard
LC127 Word Ladder
LC934 Shortest Bridge
LC433 Minimum Genetic Mutation

A-star search

LC773 Sliding Puzzle

Very Large Object

External Sort

Method

Two Pointer

Window

Squeeze

Three Sum

Fast and Slow

LC109：找linked list中间值
判断linked list成环

Two Way Scan

DFS

Move Inside an Array Or maybe can solve by DP

Permutation / Combination

LC47 Permutations II

BFS

Stack

Heap

LC23 Merge k Sorted Lists

DP

Move Inside an Array

经典DP寻路，如果是DP需要上面和左边的点的信息，只需要先行后列遍历即可

DP两种方法

  1. 从底向上：填表
  2. 从顶向下：DFS加填表

Tricky DP

LC239. Sliding Window Maximum

max_left(i) and max_right(i)

LC239. Sliding Window Maximum

LC rain water

Hash Table / Prefix Tree / Bitmap

Two Sum
Word Search II

Linked List / Deque

报数问题
Sliding Window Maximum：Deque

实现一个带tag的queue，push的时候有tag，pop的时候可以指定tag，也可以不指定

Sort

Merge Interval

Random

Greedy

Search on a Matrix
Greedy 总结

LC53 Maximum Subarray

Input: [-2,1,-3,4,-1,2,1,-5,4],
Output: 6
Explanation: [4,-1,2,1] has the largest sum = 6.

Binary Search

对于一个有序数组，其中一个数字出现了一次，其他都出现了两次，求出现一次数字的位置
划分数组使得子数列的和的最大值最小

Union Find

Other Trick

Zig-Zag Print

Another Zig-Zag Print

Bucket

LC239. Sliding Window Maximum

google rain

关于search tree的思考

search tree可以支持add, delete, findmax, find均logN

Heap + Lazy Deletion

用一个map+一个heap，可以实现一种数据结构
add, delete, getmax平均logN
在find sliding window maximum
LC716. Max Stack都可以用

另外的用处是在dijkstra

如果只是一个heap，不支持任意delete

关于linked list

在需要O(1)插入删除的时候可用

关于hash table

在需要存储key-value pair的时候可用，比如对数组建立索引

如何解决一个动态集合的max问题

比如LC716. Max Stack
和sliding window maximum

如果这个集合的插入/删除完全没有规律，可以用heap+lazy deletion，或者search tree
如果有规律，可以事先预存好次优的max
比如sliding window maximum，

二分查找

TODO

LC145
LC773
LC315

Segment tree??

还没有归类的
sliding window maximum

Unclassified